GitHub World
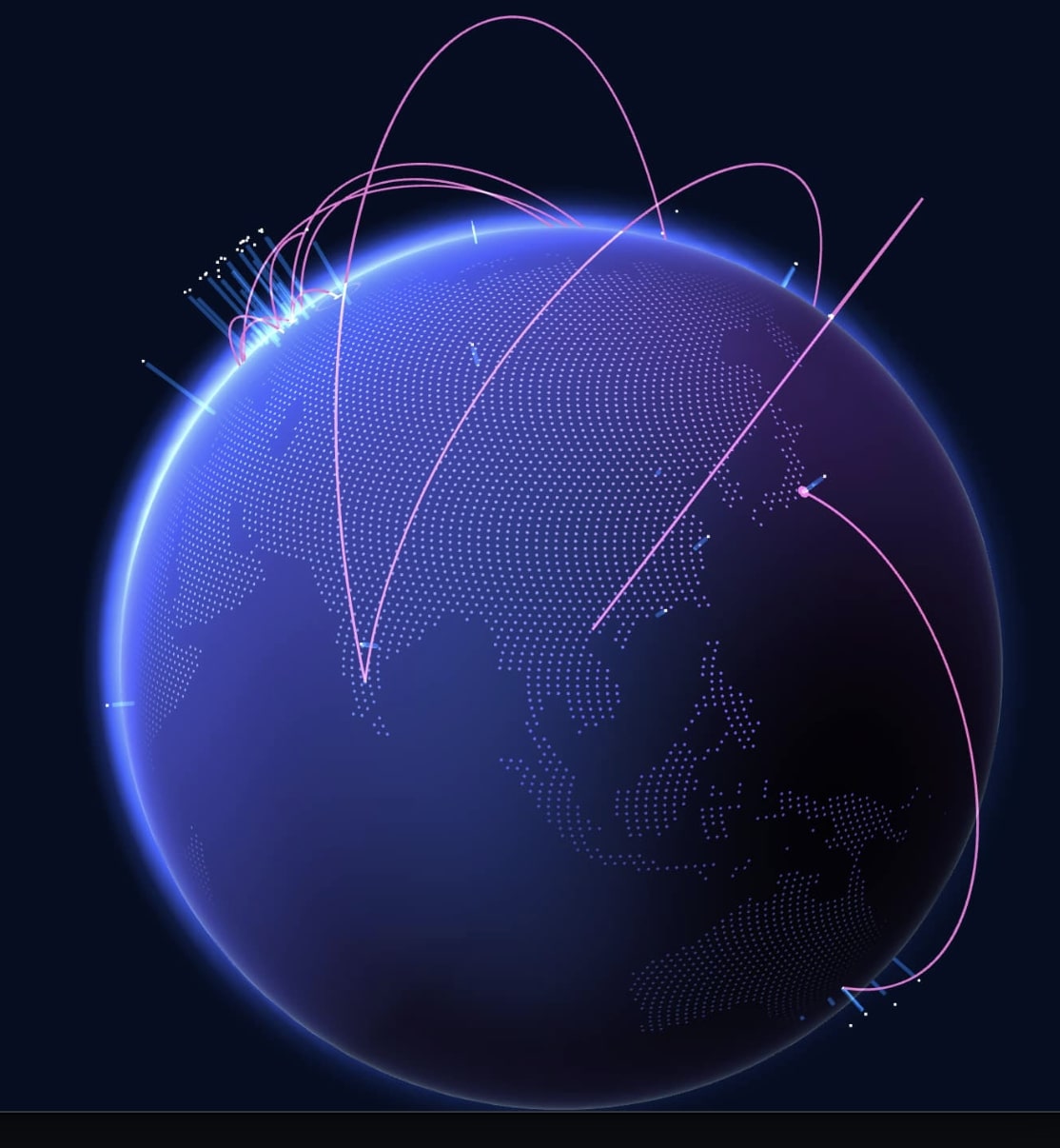
What I Learned
This was one of my first mini-projects. It began with a curiosity about 4D shapes, but I realized that understanding how to display a 3D shape on a 2D screen would be a better MVP.
I began by plotting points on the surface of a cirlce and then converting that to the points on a sphere.
The equation for a sphere in three-dimensional space is x2 + y2 + z2 = r2. Given a known x and y coordinate, we can calculate the corresponding z value using the rearranged equation: z = ±√(r2 - x2 - y2). The ± represents the two points where a line intersects a sphere, one entering (+) and one exiting (-).
By randomizing x and y coordinates and calculating the corresponding z values, I plotted these points on a canvas. However, the result resembled a flat circle rather than a sphere.
The issue was that without motion or shading, the sphere lacked depth. Similar to how vantablack absorbs light and makes 3D objects appear 2D. To create the illusion of depth, I needed to hide points with negative z values (those "behind" the sphere) and change the size of points near to z = 0 to appear smaller.
Once these adjustments were in place, the sphere looked more convincing—but it still felt static. To bring it to life, I added rotation.
Rotating the sphere along its y-axis is straightforward: for a given angle θ, the new coordinates are calculated using trigonometry. Specifically:
x' = x * cos(θ) - z * sin(θ)z' = z * cos(θ) + x * sin(θ)
To understand where this equation comes from, first we have to understand that when we rotate around the y-axis, we dont change the y value on the screen at all.
Next, envisoin a slice of the sphere at a point of 'y' and you'll actually have a disc. On this disc, all we are doing is moving the points from (+x,0) -> (0,+z) -> (-x,0) -> (0,-z)
So lets focus on (+x,0) -> (0,+z)
As the point travels round the circle, the change on x by the rotation is x*cos(0). But as it turns, the z amount gets transformed into the x amount also to the tune of - z * sin(0)
To check that x' = x * cos(θ) - z * sin (θ) = x * cos(90) - z * sin (90) = x * 0 - z * 1 = 1 * 0 - 0 * 1 = 0
As the point travels round the circle, the change on z by the rotation is z*cos(0). But as it turns, the x amount gets transformed into the z amount also to the tune of + x * sin(0)s
To check that z' = z * cos(θ) + x * sin(θ) = z * cos(90) + x * sin (90) = z * 0 + x * 1 = 1 * 0 - 1 * 1 = 1 (this in our case would be +z)
(I later changed the direction of the points to spin the opposite way by changing x' to be x' = x * cos(θ) + z * sin(θ). This is so that the earth rotated in the right direction!)
When combining multiple transformations (like spinning along two axes), it becomes easier to manage these calculations using matrices. For anyone curious about matrix transformations, I highly recommend 3Blue1Brown’s excellent video series on the topic.
To maintain proper orientation, I limited vertical rotation so the globe always appears upright. I also mapped real-world land boundaries using latitude and longitude, converting them to Cartesian coordinates to plot on the sphere.
To optimize performance, I wrote a script to reduce the number of plotted points by sampling based on circle intersections along the y-axis. This simplification also explains why some land features appear slightly exaggerated.
With all these pieces in place—along with a splash of color—I finally had a working, interactive globe that I was proud to call finished.
Future Plans
Next, I’d love to explore visualizing a 4D hypersphere. Using x and y for the 2D screen projection, z for depth (as with the 3D sphere), and w as a color gradient ranging from black to white, I aim to bring a slice of the fourth dimension to life.